A friendly guide to understanding a primary research paper: the proof of the Dinitz conjecture

by Chartreuse Goose

Table of contents

Introduction ↩︎

This is a guide for people who want to learn how to understand a primary research paper in math, specifically in the area of graph theory, one of the more accessible areas of math. If that is the case, this is the guide for you! The Dinitz conjecture was a famous open problem for several decades, and concerns list coloring on a square \(n \times n\) grid. Specifically, if you have an \(n \times n\) grid, and you have a fixed list of \(m\) colors, where \(m \ge n\) and for each vertex, you arbitrarily assign \(n\) colors out of the \(m\) colors, is it possible to assign one color to each vertex out of each assigned list to the vertex, such that no row or column in the grid contains a duplicate color? It turns out the answer to this question is yes!

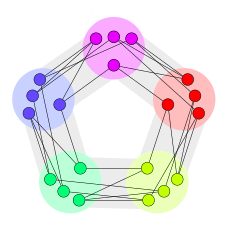
This first figure shows an example of list-coloring on an \(n = 3\) square grid, given an arbitrary assignment of \(m = 3\) colors, where it happens to be the case that there are 4 distinct colors across all the lists of colors assigned to each vertex. As such, we have labeled each unique color a number. This may not necessarily always be the case, but we will use this as a first example to illustrate the equivalence between a "color" and indexing the color with a natural number. Boxed in gray per each vertex yields one possible solution for coloring each vertex such that no row or column contains the same color/number.

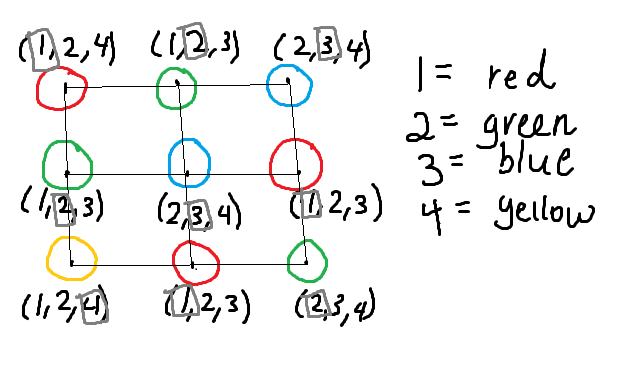
The second set of figures shows two examples of list-coloring on an \(n = 3\) square grid, given an arbitrary assignment of \(m\) colors to each vertex, where \(m = n\) as well as when an example when \(m > n\), namely \(m = 4\). It's good to note that the set that the \(m\) colors are being drawn from, is the whole set of natural numbers, not just the consecutive list of numbers \(1,2,3...m\)--as such there are numbers way larger than \(m\) appearing in the list for each vertex, in this particular assignment. In these two particular arbitrary assignments, we were able to find solutions, a choice of color for each vertex, circled in red, so that no row or column contains the same color. But one may be curious as to how we would prove such a solution exists for any arbitrarily drawn list of colors assigned to each vertex..

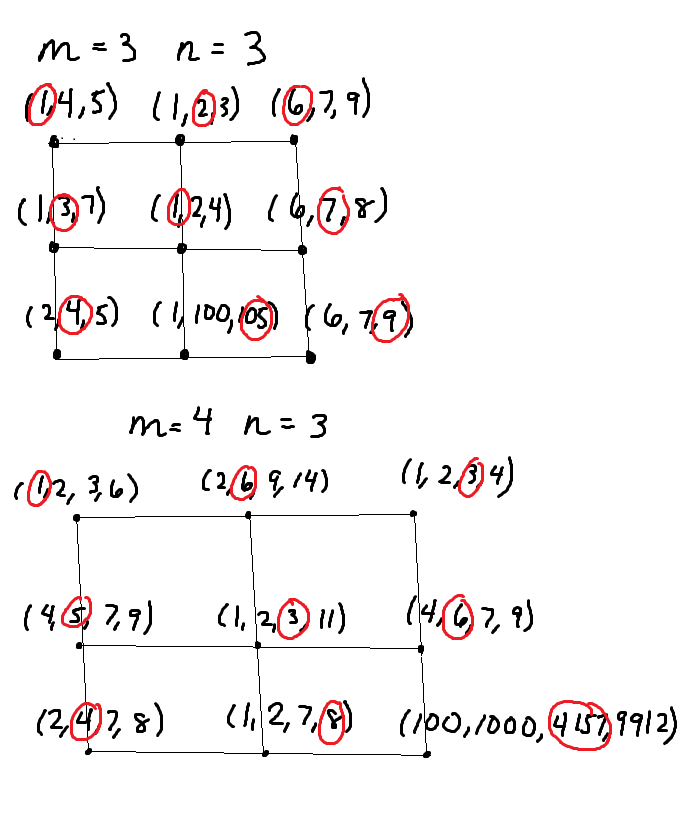
What's interesting to observe is that the line graph of \(K_{n,n}\) is exactly the sort of \(n \times n\) grid we are interested in list coloring. To make this equivalence clear, below is an image that may be helpful.

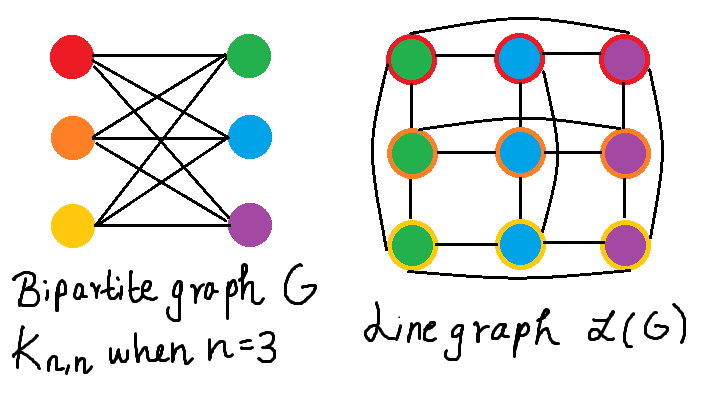
On the left is an instance of the bipartite graph \(K_{n,n}\) when \(n = 3\). Each vertex is given a different color so that it visually makes sense when consider the edge between two colors in the bipartite graph, the line graph contains the vertex that is a mixture of the two colors. For example, the edge between the red and the green vertex in the bipartite graph is represented as a vertex with a red border and a green filling in the line graph. All the edges incident to the edge connecting the red and green vertex in the bipartite graph, are incident to edges that contain a red or green vertex--and in the line graph, it can be clearly seen that the red bordered and green filled vertex (which represents the edge in the bipartite graph between the red and green vertex), has edges to 4 other vertices that have either a red border of a green filling. This coloring of the vertices is for easy visualization of the equivalence between the line graph of the bipartite graph and the graph we are hoping to work with for the Dinitz conjecture. In fact, the first person to prove the Dinitz conjecture made use of a theorem, concerning the line graphs of bipartite graphs, published 6 years prior to his result, as foundational for his result. By doing so, he actually proved a much more generalized version of the Dinitz conjecture.

The mathematician Fred Galvin famously gave an original and first proof for the Dinitz conjecture, and this guide covers the background needed to understand his result. The way I would suggest using this guide is to first give a quick look through of Galvin's succinct proof. Pending any confusions from the reader, reading the Definitions and Beginner problems sections of this guide will aid in clarifying definitions and quizzing oneself on the way in which they are to be used, aiding in gaining foundation to make the paper easy-reading for anyone! After these two sections are covered to one's liking, the Problems and Challenge problems sections cover some harder questions as well as how to interpret the two main results in the paper. Once the reader has covered these four sections, they will be well equipped to read through this succinct paper. The concluding My open questions section outlines some of the pending areas of investigation I had. One of my curiosities is concerning the details of an algorithm for actually producing a valid list coloring, as the proof outlined in the paper outlines only the existence of one.

Definitions ↩︎

Beginner problems ↩︎

Problems ↩︎

Challenge Problems ↩︎

Dinitz' conjecture can be reframed using the terms from graph theory of (\(f\):\(g\))-choosability, chromatic number/index, orientation, and line graph! Dinitz' conjecture is: 'Is it true, that for any graph \(D\) where there are \(n^2\) vertices are laid out as grid points on a square, and for any vertex in row \(i\) column \(j\), \(v_{ij}\) has edges to every \(v_{kj}\) and \(v_{il}\) for every \(k,l\) in the set \({1..n}\) excluding \(i\) and \(j\), respectively, and an arbitrarily drawn subset \(C_{sub_v}\) sized \(n\), drawn out of a constant \(m\) sized set (where \(m \ge n\)) of colors, it is possible to choose a color \(c_v\) and assign it to \(v\), out of each \(C_{sub_v}\), such that \(D\) is colorable using the set formed by the set of \(c_v\)?' Since \(D\) can be also seen as any orientation of the line graph of the bipartite graph \(K_{n,n}\), if we were to show that \(D\) is \(n\)-choosable (aka (\(f\):\(g\))-choosable for constant functions \(f\) and \(g\) assigning \(n\) and 1 to each vertex, respectively), then we will have proven the Dinitz conjecture. This is because if we can show that out of an infinite number of colors, drawing \(n\) colors arbitrarily and assigning to each vertex of \(D\) and showing a vertex can be selected out of each of the lists in a graph colorable way, then we will have immediately shown this result for drawing \(n\) colors out of \(m\) colors where \(m \ge n\).

Lemma 2.1 is essential in proving the Dinitz conjecture in Galvin's paper. Lemma 2.1 in Galvin's paper states: "Let \(D\) be a digraph in which every induced subdigraph has a kernel. If \(f,g : V(D) \to \mathbb{N}\) are such that \(f(v) \ge \sum_{u \in N[v]} g(u)\) whenever \(g(v) > 0\), then \(D\) is (\(f\):\(g\))-choosable". Below is the body of the proof and some exercises based on it to exercise your thinking!

Let \(V = V(D)\). We use induction on \(\sum_{v \in V} g(v)\). Let \(W = \{v \in V: g(v) > 0\}\). Let sets \(A_v\) (for \(v \in V\) with \(|A_v| = f(v)\) be given. Choose any \(c\) in \(C = \cup_{v \in W} A_v\). Let \(S = \{v \in W: c \in A_v\}\). Let \(K\) be a kernel of \(S\). Define \(g': V \to \mathbb{N}\) by setting \(g'(v) = g(v) - 1\) for \(v \in K\), and \(g'(v) = g(v)\) for \(v \notin K\), and let \(f'(v) = |A_v\setminus\{c\}|\). Then \(\sum_{v \in V} g'(v) < \sum_{v \in V} g(v)\) and \(f'(v) \ge \sum_{u \in N[v]} g'(u)\) whenever \(g'(v) > 0\). By the induction hypothesis, \(D\) is (\(f'\):\(g'\))-choosable. Thus there are sets \(B'_u\) and \(B'_v\) that are subsets of \(A_u\setminus\{c\}\) and \(A_v\setminus\{c\}\), respectively, such that for any \(u\) and \(v\) that share an edge, \(B'_u \cap B'_v\) is empty. If we can show that adding back a color to the appropriate \(B'\) sets will result in every \(v\) being assigned a subset \(B'_v\) that has size \(g(v)\) and is a subset of \(A_v\), then we will have shown that \(D\) is (\(f\):\(g\))-choosable. Define sets \(B_v\) by setting \(B_v = B'_v \cup \{c\}\) if \(v \in K\), and \(B_v = B'_v\) otherwise. Then \(|B_v| = g(v)\) for every \(v \in V\), and \(B_u \cap B_v\) is empty if \(u\) and \(v\) share an edge.

Now try giving Galvin's proof of the Dinitz conjecture another look and see if the below makes sense regarding how to prove the main result of the paper!

It is shown in an earlier result (which is one of my open questions/areas to explore, that is clearly explained in the proof of Maffray's theorem), that the line graph of the bipartite graph \(K_{n,n}\), is perfect, which is one of my open questions. The statement "every line graph of a multigraph is perfect iff the line graph is solvable", yields:

Then, as can be seen in Theorem 4.1 in the paper, we can very cleverly choose a particular orientation \(D\) of the line graph of \(K_{n,n}\) for which it is convenient to show that \(D\) is normal, and show that \(D\) has the property that the maximum outdegree for any vertex in \(D\) is \(n - 1\). Finally with all these preconditions we can invoke Lemma 2.1 to show that \(D\) is \(n\)-choosable. Note that by showing that any particular orientation of the line graph of \(K_{n,n}\) is \(n\)-choosable, we will have proved the Dinitz conjecture--this is because the definition of \(n\)-choosable invokes the property of two vertices sharing an edge in any particular direction.

My open questions ↩︎